栈和深度优先搜索

Copyright

本页面贡献者：lengwind, HBlade。 本页面内容遵循 MIT 协议，转载请附上原文出处链接和本声明。

栈

  • 一种数据结构

  • 特性：后进先出（如同子弹弹匣上子弹一样，先放进去的子弹是在最下层的，最后才会被打出来；而最后放进去的子弹是最上层的，会最先打出来）

栈的相关概念：

  1. 栈顶与栈底：允许元素插入与删除的一端称为栈顶，另一端称为栈底。
  2. 压栈：栈的插入操作，叫做进栈，也称压栈、入栈。
  3. 弹栈：栈的删除操作，也叫做出栈。

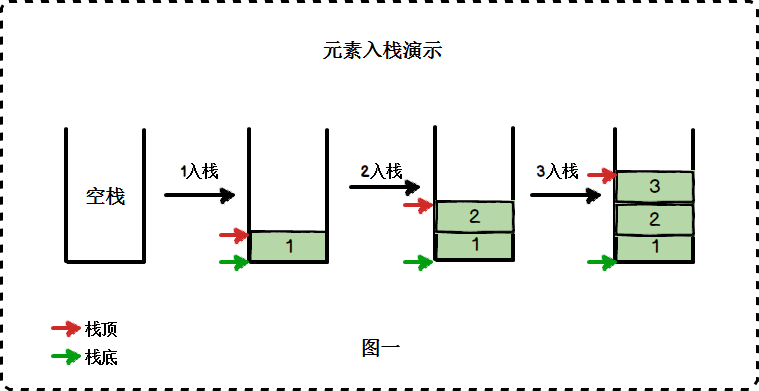
例如我们有一个存储整型元素的栈，我们依次压栈：{1,2,3}

instack.png

在压栈的过程中，栈顶的位置一直在“向上”移动，而栈底是固定不变的。

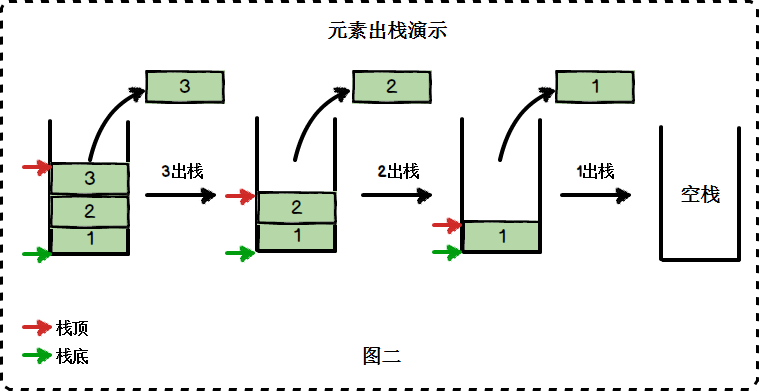
如果我们要把栈中的元素弹出来：

outstack.png

STL就有栈，不需要大家重新手写一个栈。头文件： 

1
#include <stack>
调用： 
1
2
stack < int > s;
stack < char > s;

一些常用的关于栈的函数：

  • top() 返回栈顶部的元素
  • push(x)插入元素x到顶部
  • pop()弹出顶部元素
  • size()返回栈中元素个数
  • empty() bool类型，如果栈为空返回true,否则返回false

调用只需要把定义出来的栈对象如s，使用s.top(),s.push(1),while(!s.empty())……即可

栈的应用

1.括号匹配

通过使用栈可以很简单的去判断一个括号表达式是否合法

() , (()) , )()

具体步骤:

1). 首先新建一个空栈，遍历整个表达式

2). 遇到左括号时，将对应下标入栈

3). 遇到右括号时，检查栈是否为空，如果不为空那么弹出栈顶，否则表达式不合法

2.后缀表达式

我们日常见到的数学表达式如 a + b , a * (b + c) 等都是中缀表达式

而 a b + , a b c + *是对应的后缀表达式

通过栈 可以将中缀表达式转化为后缀表达式，很方便的得到表达式的计算结果，通过这个原理可以实现一个简易的计算器

具体实现算法：

1). 初始化两个空栈：运算数栈A，运算符栈B，遍历整个中缀表达式

2). 遇到运算数 a 直接入运算数栈A (a -> A)

3). 遇到运算符号 $ 判断 当前运算符的优先级 > 栈顶的运算符的优先级，

​ 如果满足条件就入栈，否则将B栈顶符号出栈，并取运算数栈A的栈顶元素a和次栈顶元素b（也就是前两个元素），进行相应的运算a$b,并将运算结果入栈A

4). 如果遍历完表达式了，而运算符栈B不为空，那么将B栈顶符号出栈，并取运算数栈A的栈顶元素a和次栈顶元素b（也就是前两个元素），进行相应的运算a$b,并将运算结果入栈A

最终表达式的运算结果就是栈A的栈顶元素

注意:

如果是左括号那么不用判断优先级直接入栈，是右括号那么一直弹出栈顶直到遇到左括号，将左括号也弹出，结束。

如果遇到运算符而栈顶是括号，那么直接不用判断优先级直接入栈。

3.中断，子程序调用等等方面应用广泛

深度优先搜索 DFS

深度优先搜索算法（英语：Depth-First-Search，简称DFS）

定义：是ACM中一种十分常见和常用的搜索算法

方式：一般通过递归函数的方式，来搜索每一个需要的状态，去得到有用的信息，进而更新答案。

一般的搜索函数包括：

1.边界条件（搜索终止的条件，一定要注意设置好边界条件不然容易死递归）

2.递归主体

3.递归分支

1
2
3
4
5
6
void dfs(int u,int dep)
{
    if(u == dep) return ; ///边界条件
    xxx ///搜索的主要内容
    dfs(u + 1,dep); ///搜索的分支
}

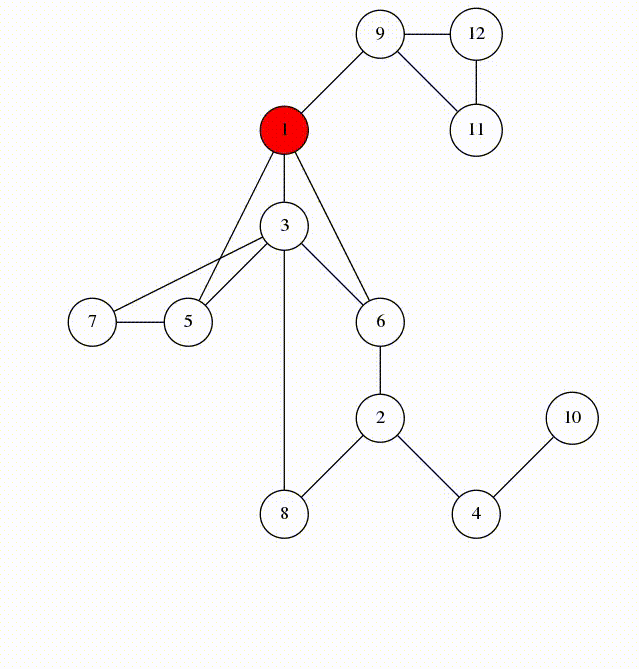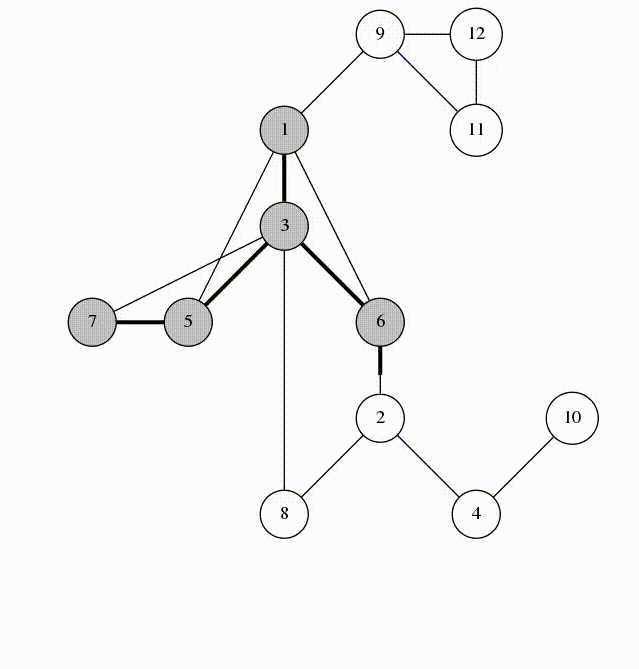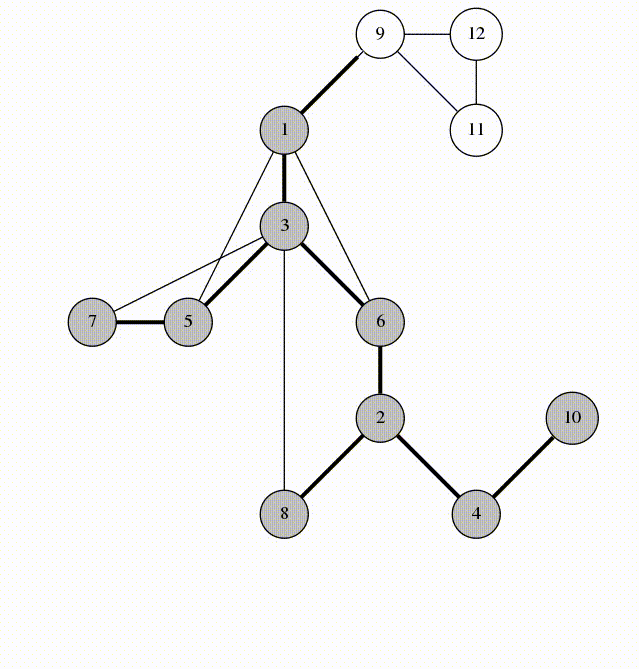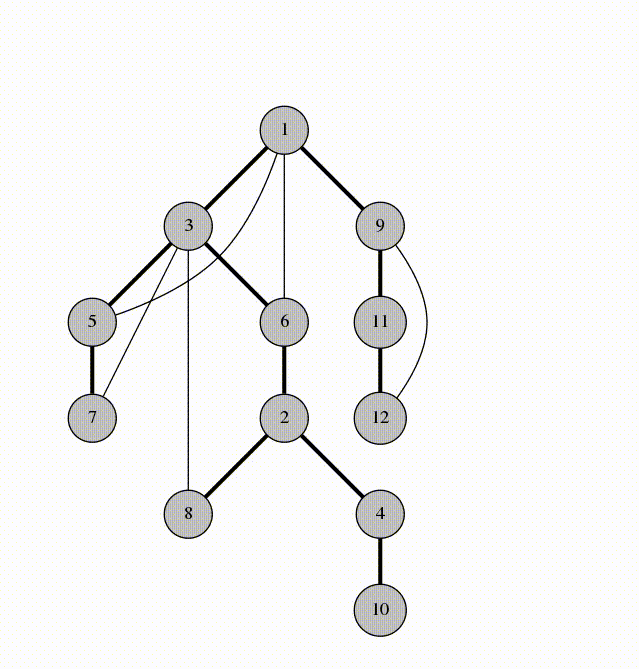
DFS搜索的过程其实是一种树型结构，一般称为DFS树。

dfs_tree.gif

DFS举例

1. DFS枚举子集

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
#include<bits/stdc++.h>
using namespace std;
const int N = 20;
bool used[N];
int a[N];
int n;
vector<int>v;
void DFS(int u) //u表示现在搜的是第u个元素(编号0~n-1)
{
    if(u == n) ///递归终止条件
    {
        for(int i : v) cout << i + 1 << ' ';
        cout << endl;
        return;
    }
    //搜索的分支有两个
    ///不选第u个元素
    DFS(u + 1);

    ///选第u个元素
    v.push_back(u); //进行操作
    DFS(u + 1);
    v.pop_back(); //回溯还原现场
}
int main()
{
   cin >> n;
   DFS(0);
}

--

2.DFS枚举全排列

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
#include<iostream>
#include<algorithm>
using namespace std;
const int N = 20;
bool used[N]; //全局bool数组记录某个数是否被选过
int a[N];
int n;
void DFS(int u) //u表示现在搜的是第u个元素(编号0~n-1)
{
    if(u == n) //边界条件 此时说明一个长度为n的排列已经枚举出来了
    {
        //直接输出枚举的排列即可
        for(int i = 0; i < n; ++ i) cout << a[i] + 1 << ' ';
        cout <<endl;
        return;
    }
    for(int i = 0; i < n; ++ i)
    {
        if(!used[i]) 
        {
            used[i] = 1, a[u] = i; //标记
            DFS(u+1);
            used[i] = 0, a[u] = 0; //回溯还原现场
        }
    }
}
/*
dfs(0):
used[0] = 1, a[0] = 0;
dfs(1):
used[1] = 1, a[1] = 1;
dfs(2):
used[2] = 1, a[2] = 2;
dfs(3)  > 0 1 2 
*/
int main()
{
   cin >> n;
   DFS(0);
}

3.八皇后问题

八皇后问题（英文：Eight queens），是回溯算法的典型案例。

问题表述为：在8×8格的国际象棋上摆放8个皇后棋子，使其不能互相攻击，即任意两个皇后都不能处于同一行、同一列或同一斜线上，问有多少种摆法。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
int n,ans;
int col[N], djx[N], ndjx[N];
void DFS(int u) //DFS记录的状态是行号
{
    if(u == n)  //如果深搜到了第n行，说明0~n-1行都放置了皇后
    {
        //那么可行解+1
        ++ans; return;
    }
    //枚举当前行u的列号从0~n-1
    for(int i = 0 ; i < n; ++ i)
    {
        if(!col[i] && !djx[i + u] && !ndjx[i - u + n]) //如果当前列，当前位置的主对角线和副对角线都没有皇后
        {
            col[i] = djx[i + u] = ndjx[i - u + n] = 1; //标记放置了皇后
            DFS(u + 1); //继续往下深搜
            col[i] = djx[i + u] = ndjx[i - u + n] = 0; //回溯还原现场
        }
    }
}

4. 连通问题

二维地图DFS,假设给你一片二维平面上的草地，其中'#'表示草，'.'表示荒地，请你去求所有连通的草地数目，上下左右在一起的草地算连通。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
const int N = 204;
char mp[N][N];
bool st[N][N];
int n,m; //n行m列的地图
int go[4][2] = //上下左右四个方向
{
  {-1,0},
  {1,0},
  {0,-1},
  {0,1}
};
bool check(int x,int y)
{
    return x >= 1 && x <= n && y >= 1 && y <= m;
}
void DFS(int x,int y)
{
    if(!check(x,y)) return; //越界判断
    for(int i = 0; i < 4 ; ++ i)
    {
        int nx = x + go[i][0], ny = y + go[i][1];
        if(check(nx,ny) && !st[nx][ny] && (mp[nx][ny] == '#') )
        {
            st[nx][ny] = 1;
            DFS(nx,ny);
        }
    }
}

拓展知识：

C++ STL