

线段树

Copyright

本页面贡献者：YanhuiJessica。本页面内容遵循 MIT 协议，转载请附上原文出处链接和本声明。

简介¶

线段树是二叉树形数据结构，每个节点代表一个区间或线段。它能解决树状数组能解决的问题，也能解决树状数组不能解决的问题（ヽ(Φˋ口ˊΦ)ノ树状数组尊严何在？），当然，相比树状数组，线段树代码量会稍微多一点~

例子¶

我们以数组 $A[\,] = \{1, 2, 3, 6, 5, 4\}$ 为例，假设需要维护的是区间最大值，那么构成的线段树如下：
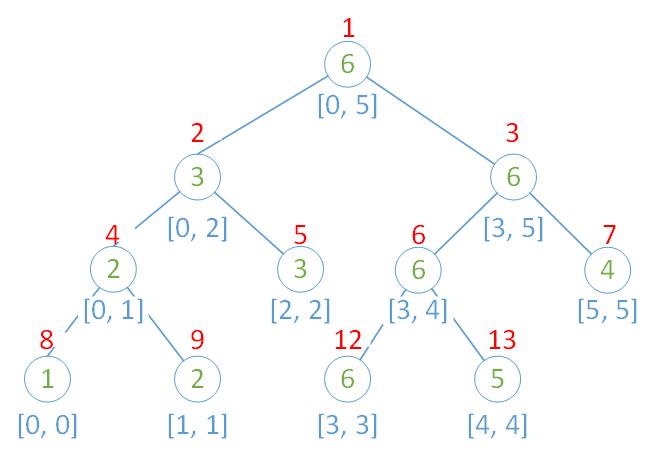
每个节点代表一个区间，节点中的值是该节点所管理区间的最大值
红色数字是每个节点的下标。在线段树中，每个左孩子的下标都是父亲节点的 $2$ 倍，每个右孩子的下标都是父亲节点的 $2$ 倍多 $1$ 。这也是为什么最下面一行叶子节点的标号直接从 $9$ 跳到了 $12$ ， $5$ 号节点虽然没有孩子，但是空间还是保留着的
这样一来，就可以把一个有 $n$ 个叶子节点的线段树看成一个完全二叉树来计算所需要的空间。对于完全二叉树 $k$ 层一共有 $2^k-1$ 个节点，第 $k$ 层有 $2^{k-1}$ 个节点，所以完全二叉树最后一层的节点数约等于前面层节点数之和。因此，无优化线段树需要 $2*2^k(2^{k-1}<n\leq2^k)$ 空间，一般会开到 $4*n$ 防 RE

基本操作¶

建树¶

typedef struct{
    // 线段树节点一般会包含的值
    v1[, v2, ...];  // 每个节点的值，和、最大值、最小值等
                    // 意义、变量数量因题而异
    lazy;   // 懒标记，区间更新时会用到
}Tree;

procedure pushup(p)
{
    // 假设维护的是最大值
    // tree 是线段树结构体数组
    tree[p].mx = max(tree[p << 1].mx, tree[p << 1 | 1].mx);
}

// 递归方式建树 build(1, 1, n);
procedure build(p, l, r)
// p 为当前节点的下标，l、r 分别为当前节点所管理区间的左右端点
{
    if(l == r)  // 左端点等于右端点，即为叶子节点，无需再向下递归
    {
        do some things;  // 为叶子节点赋初值
        return ;
    }
    mid = (l + r) >> 1;
    build(p << 1, l, mid);  // 递归构造左孩子节点
    build(p << 1 | 1, mid + 1, r);  // 递归构造右孩子节点
    pushup(p);  // 根据左右孩子的值更新父节点
}

单点更新¶

依然以数组 $A[\,] = \{1, 2, 3, 6, 5, 4\}$ 和维护区间最大值的线段树为例，假设将 $A[1]$ 的值增加 $5$ ，也就是 $A[1]$ 的值变为 $7$ ，则更新后的线段树如下：
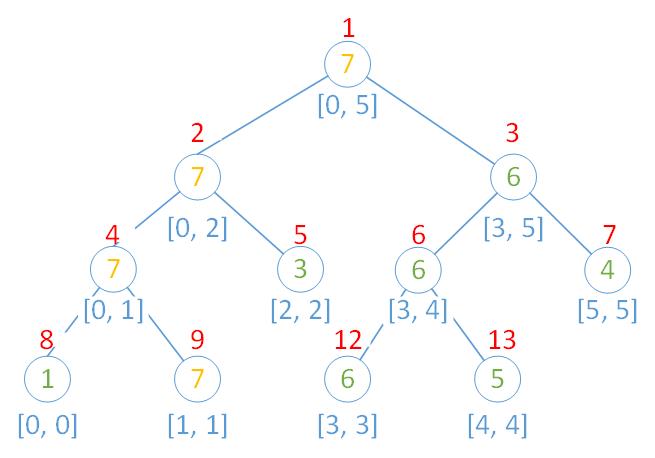
更新了 $A[1]$ 后，管理该点所在区间的所有节点都需要更新
每次更新都从叶子节点开始，假设叶子节点在第 $k$ 层，那么一共需要更新 $log(k)$ 个节点，每次更新的时间复杂度为 $O(logN)$

单点更新的伪代码如下

procedure update(p, l, r, k, v)
// k：更新的数组元素的下标
// v：更新的值
{
    if(l == r)  // 到达叶子节点
    {
        do some things; // 更新
        return ;
    }
    mid = (l + r) >> 1;
    if(k <= mid)    // 若需要更新的数组元素在左子树区间
        update(p << 1, l, mid, k, v);
    else    // 若需要更新的数组元素在右子树区间
        update(p << 1 | 1, mid + 1, r, k, v);
    pushup(p);  // 更新父节点
}

区间查询¶

依然是从根节点向下递归，如果当前节点管理的区间完全落在要查询区间内，则无需再向下递归
查询的时间复杂度也是 $O(logN)$

伪代码如下

procedure query(p, l, r, L, R)
// [L, R] 是查询的区间
{
    if(L <= l && r <= R)
        return some things;
    mid = (l + r) >> 1;
    if(L <= mid)    // 若左子树和需查询的区间交集非空
        query(p << 1, l, mid, L, R); // 递归查询，返回值请依据具体情况处理
    if(R > mid) // 若右子树和需查询的区间交集非空
        query(p << 1 | 1, mid + 1, r, L, R); // 递归查询，返回值请依据具体情况处理
    return some things;
}

区间更新¶

树状数组中区间更新使用差分的思想，而线段树选择偷懒ΦωΦ
对于区间 $[L, R]$ 来说，每次更新都需要更新所有与之相关的线段树节点，复杂度将达到 $O(NlogN)$ (╥ω╥)

于是引进了lazy标记，也就是懒标记。每次更新只更新到更新区间完全覆盖的线段树节点区间为止，而被更新节点的子孙节点区间尚未更新，于是在被更新节点上打上lazy标记，等到子孙节点被访问前再下传，所以也叫延迟标记

procedure pushdown(p)
{
    if(lazy)  // 如果 lazy 标记存在
    {
        将 lazy 标记下传到左右孩子节点的 lazy 标记;
        // 区间和 lazy 标记的值相加
        // 区间置数则直接赋值
        依据 lazy 标记更新左右孩子节点维护的值;
        清除 lazy 标记;
    }
}
procedure update(p, l, r, L, R, v)
// [L, R] 为更新的区间
{
    if(L <= l && r <= R)
    {
        更新 lazy 标记;
        更新节点维护的值;
        return ;
    }
    pushdown(p);  // 更新子树前先下传 lazy 标记
    mid = (l + r) >> 1;
    if(L <= mid) update(p << 1, l, mid, L, R, v);
    if(R > mid) update(p << 1 | 1, mid + 1, r, L, R, v);
    pushup(p);
}

区间查询时也要记得下传lazy标记嗷~(<ゝωΦ)

参考资料¶

线段树详解 - Xenny - 博客园