可持久化线段树
Copyright
本页面贡献者:YanhuiJessica。 本页面内容遵循 MIT 协议,转载请附上原文出处链接和本声明。
- 以下主要是主席树(全称可持久化权值线段树)的内容
- 权值线段树维护区间内数组元素出现的次数
- 关于主席树和可持久化线段树的关系,参见 知乎 「个人感觉主席树是可持久化线段树的子集(小声(Φ艸Φ))」
主要用途¶
查询区间第 K 大(小)
原理¶
- 对于一个长度为 n 的序列的每个前缀(共 n 个)建立一棵权值线段树,第 i 棵树存储的是原序列 [1,\,i] 中属于权值区间 [L,\,R] 的数的个数
- 假设有序列 {4,1,3,2},那么画出来的图如下:
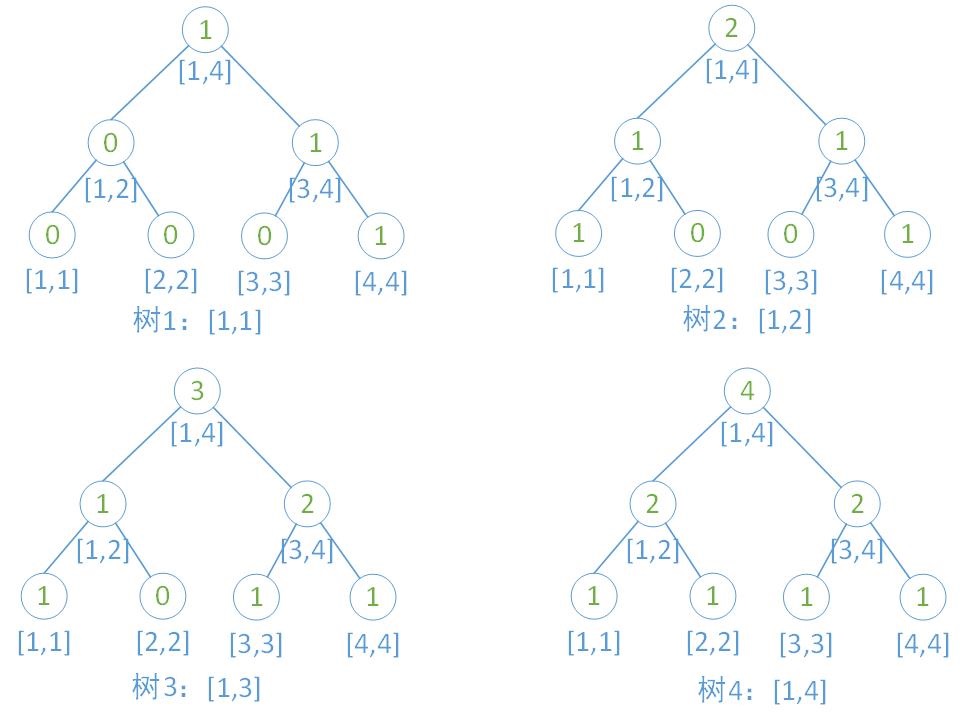
- 假设有序列 {4,1,3,2},那么画出来的图如下:
- 这么建树实际肯定是会 MLE 的(ΦдΦ╬)
- 仔细观察发现,每次加入一个数后,树上只有一条链(也就是根节点到叶子节点的路径)上节点的值会被修改。那么,实际上只需要修改 logn 个节点,剩余节点共用,真正的主席树如下(仅以前两个前缀为例):
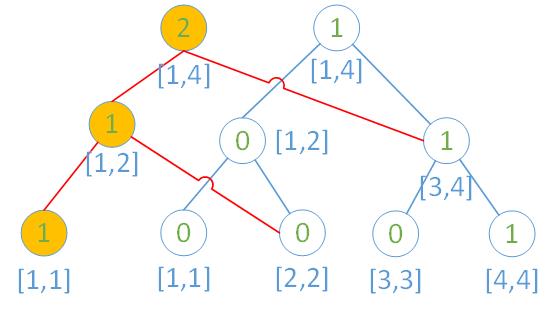
- 修改的部分另建节点,未修改的部分链接之前的
- 这样一来,就不能再用 2*x 和 2*x+1 来表示左右孩子,在主席树中使用的是动态开点的方式
实现¶
静态主席树¶
- 不变的部分使用之前的节点,更新的部分创建新节点,使用一个数组记录每次更新时树的根节点(这样就能访问指定版本了)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
update(l, r, x, &y, v) // 节点对应区间 [l, r] // x:上一棵树的节点 // y:当前树的节点,引用传参 { y = tot++; // 为 y 分配新节点,tot 记录已分配节点数 sum[y] = sum[x] + 1; // 利用上一棵树的状态来更新 if (l == r) return; ls[y] = ls[x]; rs[y] = rs[x]; // 将左右孩子初始化,值与上一棵树相同,之后遇到更新就修改 // 可以将节点信息保存在结构体中 int mid = (l + r) >> 1; // 每一时刻访问的两棵树上的节点对应区间相同 if (v <= mid) update(l, mid, ls[x], ls[y], v); else update(mid + 1, r, rs[x], rs[y], v); } - 初始主席树为空,每插入一个节点更新一次
- 查询类似于前缀和,用第 r 棵树的信息减去第 l-1 棵树的信息,就可以得到 [l,r] 区间的统计信息
- 参考线段树的查询方法,注意主席树的左右孩子表示与普通线段树不同
- 那么回到最初的问题,如何求区间第 K 大(小)呢?
- 以区间第 K 大为例,假设右孩子对应的权值区间有 x 个数,如果 x >= K,就访问右孩子,否则在左孩子询问第 K - x 大的数
1 2 3 4 5 6 7 8 9
query(k, lp, rp, l, r) // lp, rp 分别为第 l-1 棵和第 r 棵主席树的节点 // l, r 是当前节点对应的区间 { if(l == r) return l; int mid = (l + r) >> 1, cnt = sum[rs[rp]] - sum[rs[lp]]; if (cnt < k) return query(k - cnt, ls[lp], ls[rp], l, mid); else return query(k, rs[lp], rs[rp], mid + 1, r); }
- 以区间第 K 大为例,假设右孩子对应的权值区间有 x 个数,如果 x >= K,就访问右孩子,否则在左孩子询问第 K - x 大的数
- 对长度为 N 的序列进行 M 次更新,主席树的空间一般开 (N+M)*logN(当然可以直接向上取整,不排除会 MLE 的可能)
带修改主席树¶
更新¶
- 静态主席树类似前缀和,前缀和的维护修改利用到了树状数组,那么对于要修改的部分,也用树状数组维护(树状数组套主席树!)
- 建树时使用静态主席树的方式构建,当要修改历史版本时再使用树状数组
- 一共需要两个数组记录根节点,一个是原本主席树记录根节点的数组,一个记录利用树状数组维护变更值的主席树根节点
- 参考树状数组更新方法,只不过更新的操作不是对树状数组进行简单加减,而是复用主席树的
update函数(传入的是记录利用树状数组维护变更值的主席树根节点的数组)
- 从记录利用树状数组维护变更值的主席树根节点的数组下标来看,树状数组维护哪几棵主席树是与先前一致的,参见 树状数组原理说明
查询¶
- 在查询区间 [l, r] 前,先将要使用到的利用树状数组维护变更值的主席树根节点分别存储到 L[\,] 和 R[\,] 两个数组中
- 查询时,树状数组访问左右孩子和主席树同步(也就是在向下递归之前,先要更新 L 和 R 数组的值)
- 每个节点的权值区间对应数的个数需要考虑树状数组中的值(实际的值 = 原主席树节点的值 + 树状数组记录变更的值(不是变更之后的值嗷!))
树上主席树¶
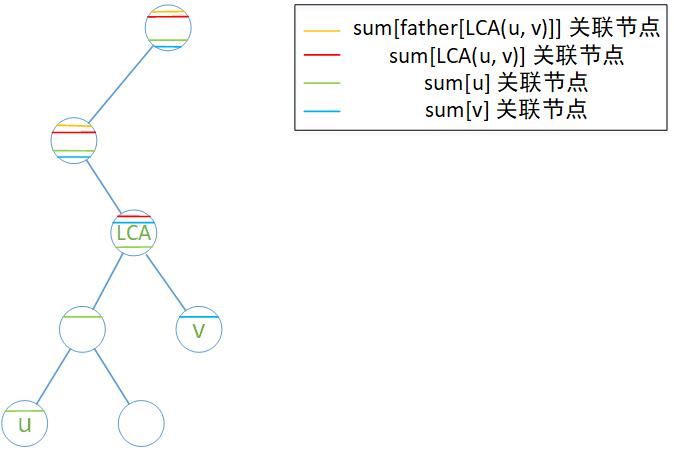
对于树上节点 u 到 v 路径上的信息,先得到两个节点的 DFS 序(可以使用 树链剖分),再通过 sum[u] + sum[v] - sum[LCA(u,\,v)] - sum[father[LCA(u,\,v)]] 获得(u、v、LCA(u,\,v)、father[LCA(u,\,v)] 表示对应主席树上的节点,sum 为各节点到根节点路径上的信息)