树链剖分

Copyright

本页面贡献者：YanhuiJessica。 本页面内容遵循 MIT 协议，转载请附上原文出处链接和本声明。

简介

  • 树链剖分将树分割成若干条链，以维护树上路径的信息
  • 树链剖分通常指「重链剖分」，剖分后的每条链为线性结构，且每条链上的节点 DFS 访问连续，可以使用线段树等数据结构维护区间信息
  • 除了用于树上两点间路径上所有点或以某节点为根的子树的修改和查询，树链剖分还可以 O(logn) 地求 LCA

重链剖分

基本概念

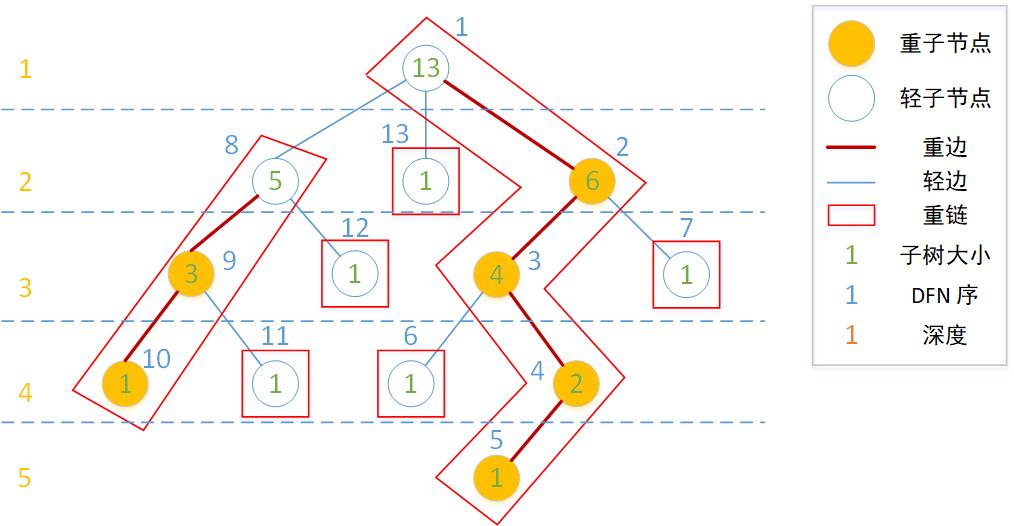
  • 重子节点：父节点的所有孩子节点中子树节点数目最多的节点
  • 轻子节点：除重子节点外的所有子节点
  • 重边：父节点到其重子节点的边
  • 轻边：父节点到其轻子节点的边
  • 重链：由首尾相接的重边构成，非重链端点的叶子节点可看作构成了长度为 0 的重链
  • DFN 序：点按照 DFS 进入节点的顺序排列的序列，是 DFS 序的子序列

树链剖分详解

实现

  • 通过两个 DFS 实现树链剖分
  • 第一个 DFS 记录每个节点的父节点、深度、子树大小及其重子节点 
     1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
    dfs1(p, pre, deep)
// p：当前节点；pre：p 的父节点；deep：当前深度
{
    dep[p] = deep, size[p] = 1, father[p] = pre;
    // dep[p]：节点 p 在树上的深度
    // size[p]：节点 p 的子树的节点个数
    // father[p]：节点 p 的父节点
    for each p's son i
    {
        size[p] += dfs1(i, p, deep + 1);
        if (size[son[p]] < size[i])
            son[p] = i
        // son[p]：节点 p 的重儿子
    }
    return size[p];
}
  • 第二个 DFS 记录节点所在链的链顶（初始为自身），重边优先遍历时的 DFS（DFN） 序，DFS 序对应的节点编号 
     1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
    dfs2(p, top)
// top：当前链的链顶
{
    tid[p] = cnt, rnk[cnt] = p, tp[p] = top;
    cnt ++;
    // tid[p]：节点 p 的 DFS 序，也是其在线段树中的编号
    // rnk[cnt]：DFS 序对应的节点，有 rnk[tid[p]] = p
    // tp[p]：节点 p 所在重链的顶部节点（深度最小）
    if (son[p]) dfs2(son[p], top);
    for each p's son i
    {
        if (i != son[p]) dfs2(i, i);
    }
}

部分性质

  • 树上每个节点都属于且仅属于一条重链
  • 重边对于每个节点都有定义，因此重链的开头节点不一定是重子节点
  • 若 (u, v) 为一条轻边，那么 size(v) < size(u)/2
  • 对有 n 个节点的树，根节点到任意叶子节点最多经过 log_2n 条轻边
  • 剖分一次的复杂度为 O(n) XD

常见应用

求最近公共祖先

如果两节点位于同一条重链，深度较浅的节点即为所求的 LCA，若不是则将两个节点中重链链顶较深的节点跳至其链顶的父节点，再次判断 

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
getlca(u, v)
{
    while(tp[u] != tp[v])
    {
        if (dep[tp[u]] > dep[tp[v]])
            u = fa[tp[u]];
        else v = fa[tp[v]];
    }
    return dep[u] > dep[v] ? v : u;
}

路径上维护

  • 用树链剖分求树上任意两点间所有节点的和、最大值、最小值等
  • 类似求 LCA 的思想，将节点上跳，跳之前使用线段树、树状数组等数据结构维护该节点到其链顶的区间
  • 以求路径区间最大值为例 
     1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
    treepath_max(u, v)
{
    mx = max(val[u], val[v]);
    while(tp[u] != tp[v])
    {
        if(dep[tp[u]] > dep[tp[v]])
        {
            mx = max(mx, query(tid[tp[u]] -> tid[u]));
            // query 为线段树或树状数组函数
            // 对 [tid[tp[u]], tid[u]] 区间求最大值
            u = fa[tp[u]];
        }
        else
        {
            mx = max(mx, query(tid[tp[v]] -> tid[v]));
            v = fa[tp[v]];
        }
    }
    mx = max(mx, query(between(u, v)));
    // 注意考虑 u 和 v 的大小关系
    return mx;
}

子树维护

  • 一些题目会要求对以某节点为根的子树进行整体操作
  • 子树中的节点的 DFS 序是连续的，可以增加一个 bottom 数组，用于记录每个节点的子树连续区间末端的节点（或其 DFN 序）
  • 子树对应的区间可以表示成：[\,tid[p],\,tid[bottom[p]]\,]

参考资料