树状数组

Copyright

本页面贡献者：YanhuiJessica。 本页面内容遵循 MIT 协议，转载请附上原文出处链接和本声明。

主要用途

  • 单点修改，区间查询
  • 区间修改，单点查询
  • 区间修改，区间查询
  • 单点修改，单点查询 (ΦдΦ╬)
  • 求逆序对

原理

  • 树状数组中使用数组来存储值，而数组中各个元素间呈树形关系

    • e.g. 通过逐个插入的方式创建数组[1, 2, 3, 4, 5]的树状数组

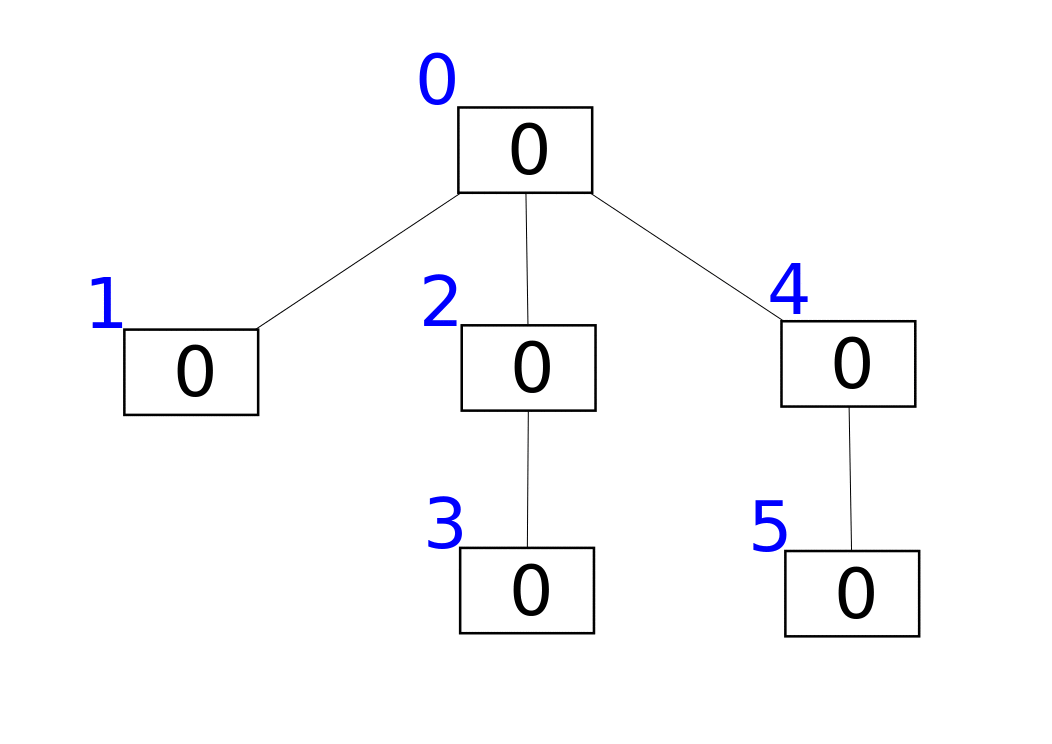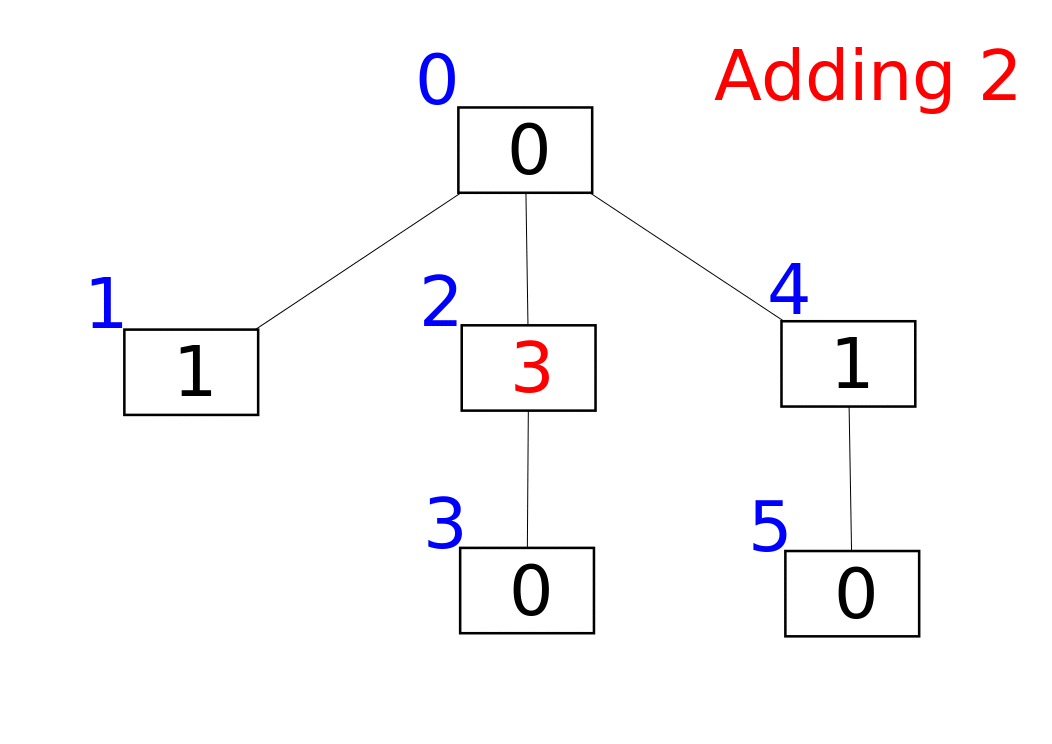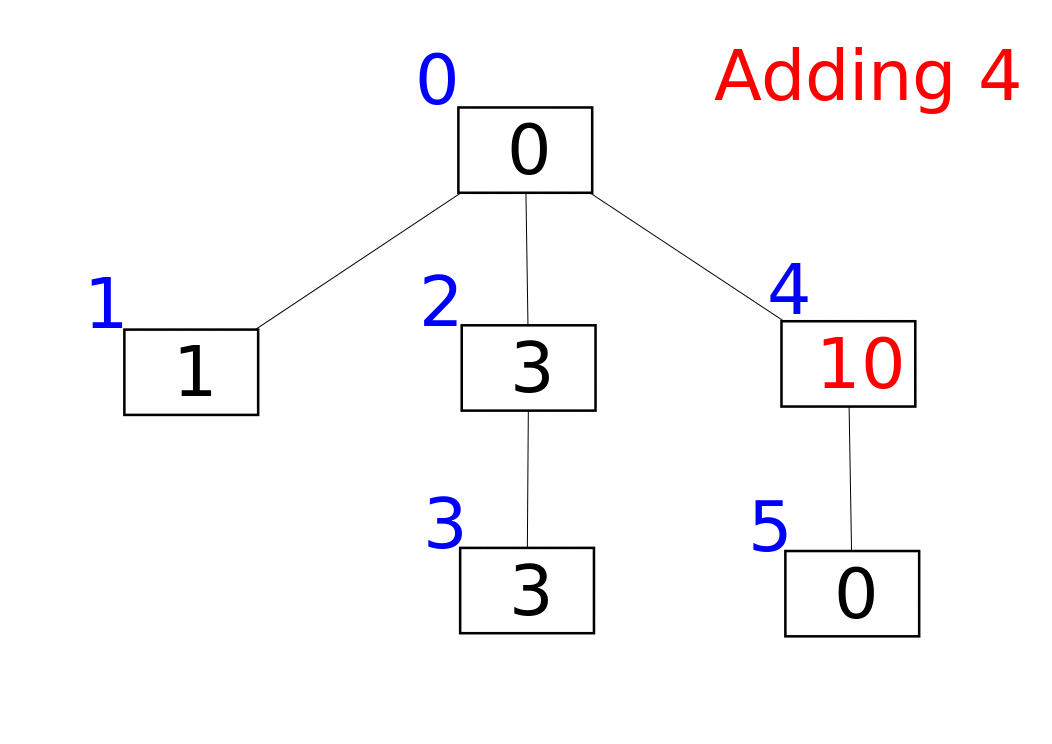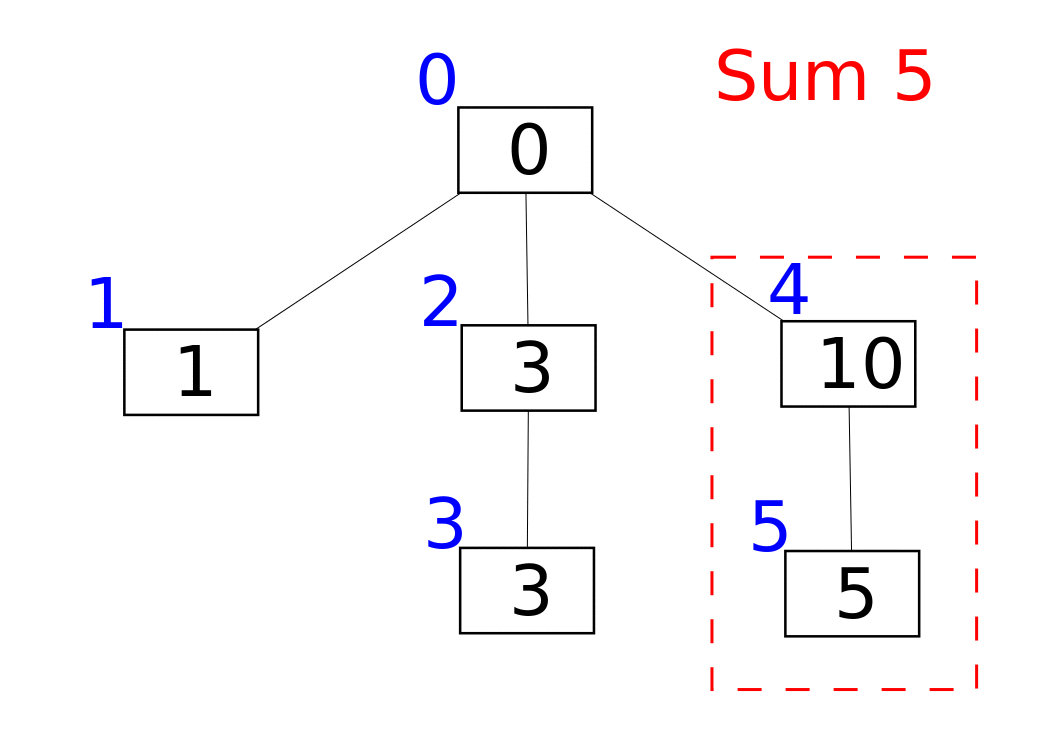
    Fenwick 树

  • 树状数组被发明是受「所有的整数都可以表示成 2 的幂和（二进制）」的启发，接下来，也将根据图片并结合二进制来解释

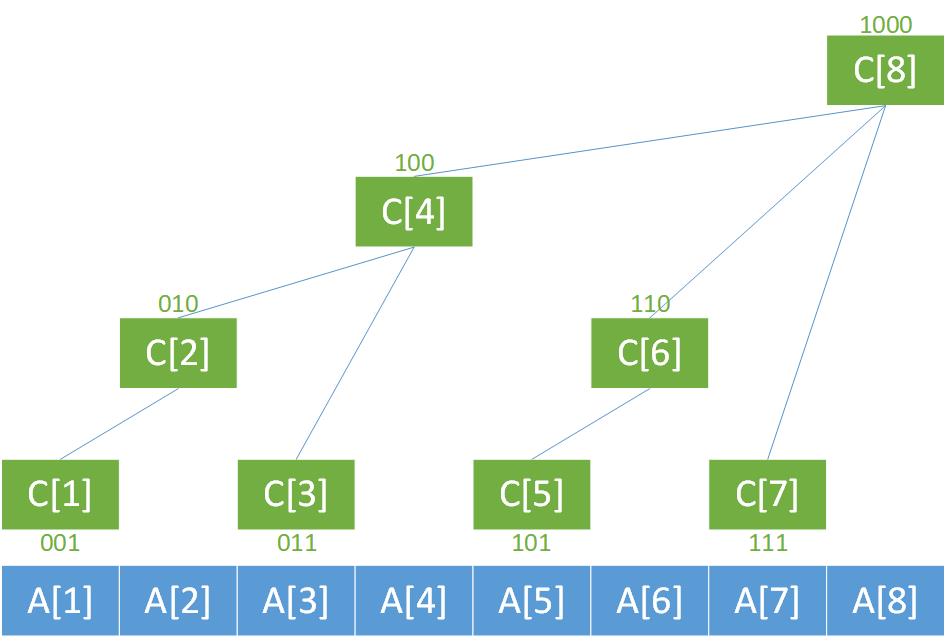
    树状数组-数组元素间关系

    • A 数组用于存储原始数据，C 数组管理 A 数组（A 数组可视情况选择是否保留，某些情况下只用 C 数组足矣）(<ゝωΦ)
      • 由图可知，C[2] 管理 A[1] 和 A[2]，C[4] 管理 A[1]、A[2]、A[3] 和 A[4]，以此类推
    • 类似于二进制，比如 5 的二进制101可以拆分成101 = 100 + 1，如果要求 A[1] 到 A[5] 的和，我们就可以直接使用 C[4] + C[5]（这样看起来好像和前缀和差不多(ΦдΦ╬) 前缀和修改起来方便吗？(Φ^Φ)）
    • 树状数组查询和修改的复杂度都为 O(log(n))

基本操作

lowbit 函数

  • 你可能已经发现了，操作的关键在于二进制中的 1，准确的说是需要知道数由 2 的哪些幂组成
  • 于是引入了函数lowbit，用来求数的二进制表达式中最低位的 1 所代表的值
    • 比如 6_{(10)}=110_{(2)}，从右往左数第一个 1 和其后的 0 组成 10_{(2)}，即代表值是 2_{(10)} 
      1
2
3
4
5
6
7
8
      // 宏定义写法
#define lowbit(x) (x & (-x))

// 函数写法
int lowbit(int x)
{
  return x & (-x);
}
  • 至于为什么是x & -x，可以学习关于补码的知识
    • 负数的补码是其对应正数二进制表示按位取反后加 1 的结果
    • 6_{(10)}\, \& \,-6_{(10)} = 110_{(2)}\, \& \,(001_{(2)} + 1_{(2)}) = 010_{(2)}

单点修改

  • 伪代码 
     1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
    procedure change(pos, v)
// pos：要修改元素的下标
// v：改变的值
{
  while(pos <= n) // n 为数组元素的数量
  {
    c[pos] += v;
    pos += lowbit(pos);
  }

  // 循环形式
  // for(i = pos; i <= n; i += lowbit(i))
  //   c[i] += v;
}
  • 除非必要，A 数组的更新可以不考虑

求和

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
procedure getsum(x)
// 求 a[1]...a[x]的和
{
  ans = 0;
  while(x)
  {
    ans += c[x];
    x -= lowbit(x);
  }
  return ans;

  // 循环形式
  // ans = 0;
  // for (i = x; i > 0; i -= lowbit(i))
  //   ans += c[i];
}
有了 A[1] 到 A[n] 的求和方法，任意区间的求和就简单了\(ΦωΦ)/。要求 [l, r] 的区间和，只需要getsum(r) - getsum(l-1)就可以了(<ゝωΦ)

进阶

区间修改，单点查询

  • 利用差分建树
  • 数组 D 用于存储 A 数组相邻两项的差值，即 D[i] = A[i] - A[i - 1]
  • 对于下面的数组 A 及其差分数组 D
    • A[] = \{1, 2, 3, 2, 1\}
    • D[] = \{1, 1, 1, -1, -1\}
  • 将 [1, 3] 区间内所有数加 2
    • A[] = \{1, 4, 5, 4, 1\}
    • D[] = \{1, 3, 1, -1, -3\}
  • 差分数组的优点就体现了，当某个 [l, r] 区间内所有数统一加减时，只有 D[l] 和 D[r + 1] 两个元素的值发生变化
  • 这样一来，C 数组就应该建立在 D 数组而非 A 数组上，区间更新则转化为更新两个点，更新函数和求和函数则不需要变

区间修改，区间查询

  • 基于 区间修改，单点查询 的差分思路，考虑如何在其构建的树状数组中求数组 A 的前缀和：
    • ∑_{i=1}^pa[i]=∑_{i=1}^p∑_{j=1}^id[j]
  • 在式子 ∑_{i=1}^p∑_{j=1}^id[j] 中，d[1] 被用了 p 次，d[2] 被用了 p-1 次……由此可以推出：
    • ∑_{i=1}^p∑_{j=1}^id[j]=∑_{i=1}^pd[i]*(p-i+1)=(p+1)*∑_{i=1}^pd[i]-∑_{i=1}^pd[i]*i
  • 接下来，只需要维护两个数组的前缀和，sum1[i]=d[i] 和 sum2=d[i] * i
  • 查询和修改的伪代码如下 
     1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
    procedure change(pos, v)
{
  for(i = pos; i <= n; i += lowbit(i))
    sum1[i] += v, sum2[i] += v * pos;
}
// 更新区间 [l, r]
// change(l, v), change(r + 1, -v);
procedure getsum(pos)
{
  ans = 0;
  for(i = pos; i; i -= lowbit(i))
    ans += (p + 1)*sum1[i] - sum2[i];
  return ans;
}

例题

参考资料